Properties of Exponents & Radicals
The exponent of a number shows how many times a number is multiplied by itself. For example, 34 means 3 is multiplied four times by itself, that is, 3 × 3 × 3 × 3 = 34, and here 4 is the exponent of 3. Exponent is also known as the power of a number and in this case, it is read as 3 to the power of 4. Exponents can be whole numbers, fractions, negative numbers, or decimals.
Properties of Exponents
The properties of exponents, also known as the laws of exponents, are used to solve problems involving exponents. The properties are:
- Product Law: am × an = am+n
- Quotient Law: am ÷ an = am-n
- Zero Exponent Law: a0 = 1
- Negative Exponent Law: a-m = 1/am
- Power of a Power Law: (am)n = amn
- Power of a Product Law: (ab)m = ambm
- Power of a Quotient Law: (a/b)m = am/bm
Example 1
- x2·x3 = x2+3 = x5
- y7 ÷ y3 = y7-3 = y4
- 4-2 = 1/42 = 1/16
- (23)3 = 23·3 = 29 = 512
- (5x)2 = 52 · x2 = 25x2
- (x/3)3 = x3/33 = x3/27
Roots and Radicals
The symbol  is called a radical sign (or surd) and is used to designate square root. To designate a cube root, a small three is placed above the radical sign,
is called a radical sign (or surd) and is used to designate square root. To designate a cube root, a small three is placed above the radical sign,  . When two radical signs are next to each other, they automatically mean that the two are multiplied. The multiplication sign may be omitted.
. When two radical signs are next to each other, they automatically mean that the two are multiplied. The multiplication sign may be omitted.
The following rules apply to radicals:
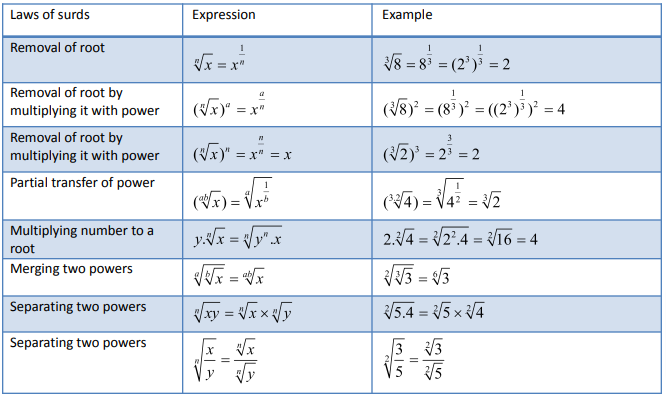
Note the similarity between these properties and standard exponent properties. This is explained by the first property: radicals are simply fractional exponents and so utilize the same properties as exponents.
Example 2
Simplify the following expressions:
- 2√3 + 3√3 = (2+3) · √3 = 5√3
- 5√2 – √2 = (5-1) · √2 = 4√2
- √32 + 3√2 = √(16·2) + 3√2 = √16 · √2 + 3√2 = 4√2 + 3√2 = (4+3) · √2 = 7√2
- √(2x2) + √(2y2) = √x2 · √2 + √y2 · √2 = x√2 + y√2 = (x+y)√2
Rationalizing Radical Fractions
The process of rationalizing a radical fraction involves removing the radical from the denominator. In mathematical notation, an expression with a radical in the denominator is irrational notation and must be rationalized. There are 2 approaches that need to be discussed:
A radical value in the denominator ⇒ in the case of [a/√x] multiply this fraction by 1 in the form of [√x/√x]:
A radical expression in the denominator ⇒ in the case of [a/(√x + b)] multiply this fraction by 1 in the form of the conjugate of the denominator [(√x – b)/(√x – b)]:



